肖庆都的博客

点点滴滴

0%

递归反转链表：拆解复杂问题

发表于 更新于 分类于 Valine：
本文字数： 1.5k 阅读时长 ≈ 1 分钟
递归实现反转链表

递归反转链表：拆解复杂问题

反转单链表的迭代实现不是一个困难的问题，但是递归实现就有些难度了。反转单链表中的一部分，是否可以通过递归实现？

本文有简单到复杂，一步一步的解决反转单链表中的一部分这个问题。

单链表节点的结构

1
2
3
4
class ListNode:
    def __init__(self, val):
        self.val = val
        self.next = None

什么叫做反转链表的一部分？意思是：给定一个区间，将链表中区间内的元素反转，其他部分不变。

反转从位置m到n的链表。请使用一趟扫描完成反转

说明

$1<= m <= n <= 链表长度$

示例

输入：1 -> 2 -> 3 -> 4 -> 5 -> NULL, m = 2, n = 4 。 输出： 1 -> 4 -> 3 -> 2 -> 5 -> NULL

注意这里的索引是从1开始的。迭代的思路大概是：先用一个for循环找到第m个位置，然后再用一个for循环将m和n之间的元素反转。但是递归解法不用任何for循环，

迭代实现思路看起来虽然简单，但是细节问题很多，不太容易写对。相反，递归实现很简洁优美，下面由浅入深，先从反转整个单链表开始讲起。

一、递归反转单链表

首先先介绍一下算法实现

1
2
3
4
5
6
7
8
class Solution:
    def reverse(self, head):
        if !head.next:
            return head
       	last = reverse(head.next)
        head.next.next = head
        head.next = None
        return last

单纯从代码上来看，有一种不知所云的感觉，甚至是完全不能理解为什么能够反转链表。下面详细解释下这一段代码

对于递归算法，最重要的就是明确递归函数的定义。具体来说，这里定义的reverse函数具体含义如下：

输入一个节点head,将（以head为起点）的链表反转，并返回反转之后的头节点。

了解函数的定义后，再来看这个问题，例如想反转这个链表：

1
2
3
4
5
6
7
8
graph LR
	h(head) --> A(1)
    A(1) ==>B(2)
    B(2) ==>C(3)
    C(3) ==>D(4)
    D(4) ==>E(5)
    E(5) ==>F(6)
    F(6) ==>G(None)

那么输入reverse(head)后，会在这里进行递归

1
last = reverse(head.next)

实际理解过程中，不要试图跳进递归中，要根据函数定义，来弄清楚这段代码会产生什么结果：

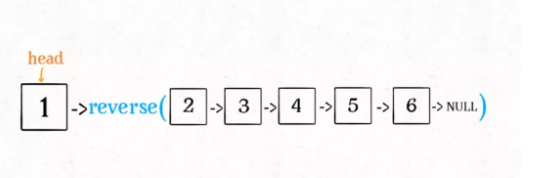
graph2

按照这个定义，这个reverse(head。next)执行完成后，整个链表应该会变成如下：

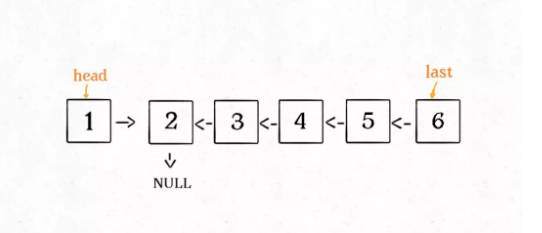
graph3

并且根据函数的定义，reverse函数会返回反转之后的头节点，这里使用last接收。

继续往下走：

1
head.next.next = head

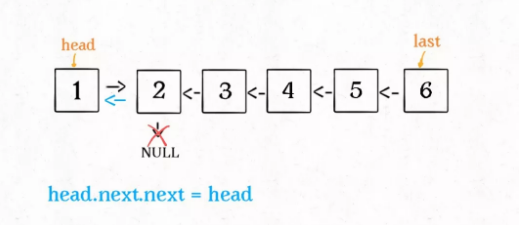
graph4

继续进行接下来的操作

1
2
head.next = None
return last

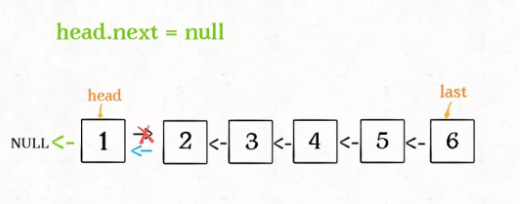
graph5

通过如上操作，整个链表就实现了反转。递归代码是非常简洁和优雅的。不过其中有两个地方需要特别注意：

  1. 递归函数要有边界值

    1
    2
    if !head.next:
        return head

    解释：如果链表只有一个节点，那么反转的时候，只有它自己。直接返回即可。

  2. 当链表递归反转之后，新的头节点是：last，而之前的head变成了最后一个节点，最后要将链表的末尾指向None

    1
    head.next = None

理解单链表的递归反转之后，后面可以继续深入进行其他操作。

-------------Thanks for your attention-------------